Get the latest news and updates from our developers and customers.
Subscribe
 15.04.2024
Entering the Chinese PLM Market: Detailed Insights
15.04.2024
Entering the Chinese PLM Market: Detailed Insights
In early March, a delegation from C3D Labs traveled to the land of dragons and pandas to participate in the Smart Production Solutions 2024 (SPS) international ...
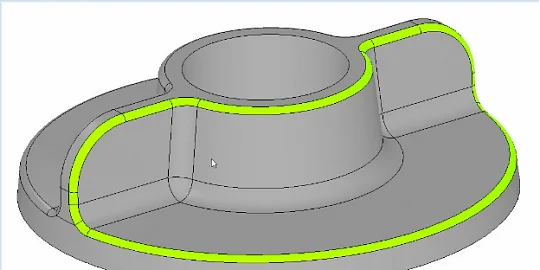 26.03.2024
Direct Modeling Updates in C3D Modeler: Changing Fillet Radius and Replacement of Faces Function
26.03.2024
Direct Modeling Updates in C3D Modeler: Changing Fillet Radius and Replacement of Faces Function
New direct modeling commands in C3D Modeler. The direct modeling tools edit imported geometry which has no history tree. The first new command is ‘Change the...
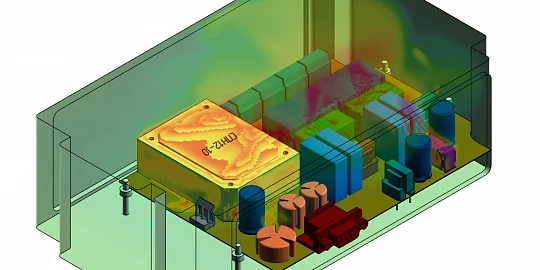 20.03.2024
C3D Vision: New Functionality and Geometric Kernel Integration
20.03.2024
C3D Vision: New Functionality and Geometric Kernel Integration
Eduard Maximenko talks about the new features in C3D Vision, the main visualization component, and presents improvements to the tools that have been around for ...
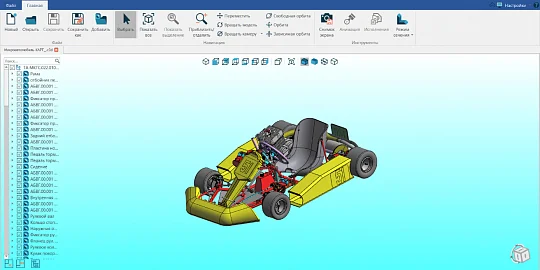 06.03.2024
C3D Viewer: New Tools and Linux Support
06.03.2024
C3D Viewer: New Tools and Linux Support
C3D Viewer is a free application from the C3D Labs product line. It is an easy-to-use 3D visualization tool that reads the most common CAD exchange formats: ACIS,...
 04.03.2024
C3D Modeler Release 117978: Changes to the Color and Optical Properties Attribute
04.03.2024
C3D Modeler Release 117978: Changes to the Color and Optical Properties Attribute
In previous versions of the C3D Modeler kernel, the color of the body and its child topological entities (faces, edges, vertices) was stored in the MbColor attribute....
 12.02.2024
Parasolid Inside: Support for New Formats and other C3D Converter Enhancements
12.02.2024
Parasolid Inside: Support for New Formats and other C3D Converter Enhancements
Alexander Spivakov, leader of the C3D Converter team, C3D Labs, talks about the purpose of the converter in the C3D Toolkit, C3D Converter use cases (migration ...
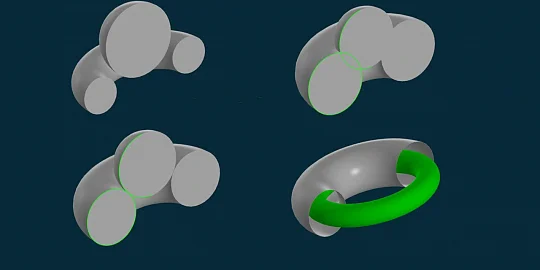 25.01.2024
Introducing a New C3D Kernel Component: C3D Collision Detection
25.01.2024
Introducing a New C3D Kernel Component: C3D Collision Detection
Sergey Belyov, Senior Math Software Engineer, C3D Labs, presents the C3D Collision Detection module, a new C3D Toolkit component. He explains what's under the hood...
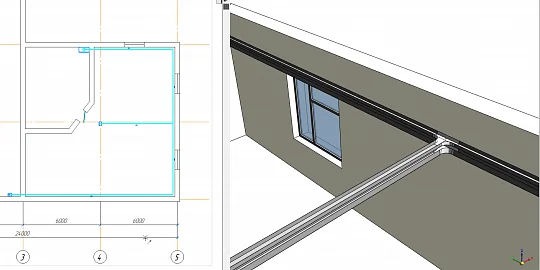 15.01.2024
C3D Vision Reinvents 2D Floor Plans
15.01.2024
C3D Vision Reinvents 2D Floor Plans
The Electric Supply & Lighting application is a design tool for industrial power supply and electric lighting projects. With the C3D Vision module, a part of...
 26.12.2023
C3D Modeler Polygonal Modeling Tools for Reverse Engineering in KOMPAS-3D
26.12.2023
C3D Modeler Polygonal Modeling Tools for Reverse Engineering in KOMPAS-3D
Reverse engineering is the rebuilding or copying of an existing product. The data source for reserve engineering is usually a scanned polygonal model. In this paper,...
 12.12.2023
C3D Solver: Parametric Drafting of 2D Patterns and 3D Assembly Modeling Improvements
12.12.2023
C3D Solver: Parametric Drafting of 2D Patterns and 3D Assembly Modeling Improvements
Alexander Alakhverdyants introduces innovations in the 2D and 3D solvers developed by the C3D Solver team. What are the solvers? Solvers are software libraries...
