Ранее в статье о новинках модуля параметризации C3D Solver 2023 мы представили функционал линейных интервальных размеров. Данный подтип основан на управляющем размере, однако имеет несколько отличий от последнего. В этой заметке мы расскажем о различиях между интервальным и управляющим размерами. В качестве бонуса анонсируем новый подтип интервальных размеров.
Появление линейных интервальных размеров
В конце 2021 года в трехмерном решателе впервые реализован интервальный подтип размера, а именно линейный (interval distance dimension).
В API C3D Solver для установки такого измерения необходимо вызвать функцию GCM_AddDistance(…), которая в качестве его значения может принимать как число, так и числовой интервал. Однако в первом случае создается управляющий размер (driving dimension), а во втором — интервальный. Чтобы понять, чем интервальный размер отличается от управляющего, рассмотрим особенности последнего.
Характерным свойством управляющего размера является то, что он задается единственным значением. При этом только пользователь имеет возможность изменять это значение как независимый параметр системы (посредством вызова функции GCM_ChangeDrivingDimension(…)), а решатель обладает возможностью лишь принимать его для исполнения.
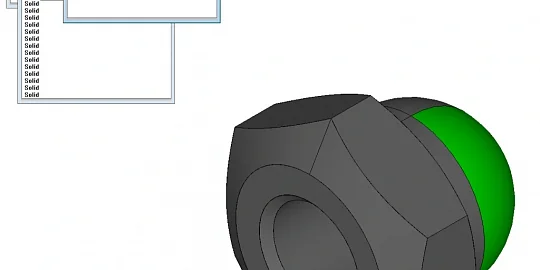
Другим свойством является то, что управляющий размер устраняет одну и более степеней свободы объектов. Например, если задать управляющий линейный размер между плоскими гранями тел, то такое измерение снимет три степени свободы, т.е. оставит одну степень свободы вращения и две степени свободы перемещения. Стоит отметить, что мы подразумеваем шесть степеней свободы у полностью свободного тела.
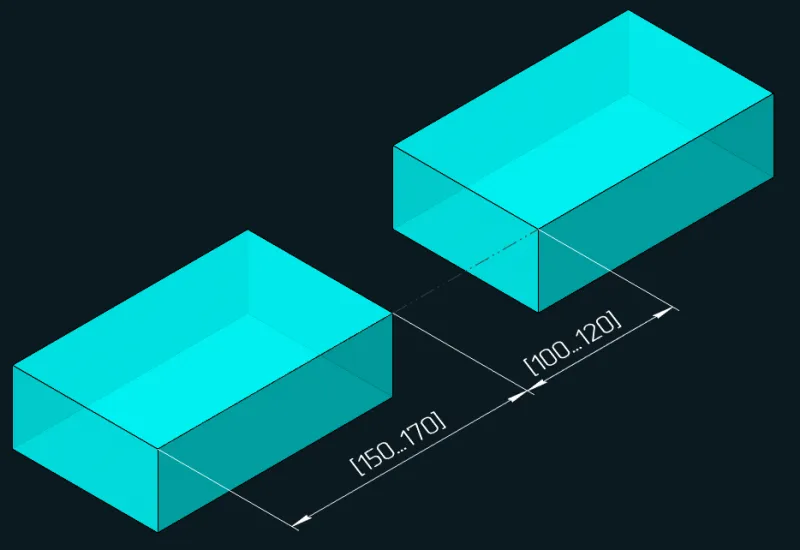
Интервальный размер, напротив, принимает не единственное значение, а любое значение из заданного диапазона [dMin, dMax]. Такой размер устраняет на одну степень свободы меньше, чем соответствующий управляющий. Например, если вышеприведенный размер между плоскостями заменить с управляющего на интервальный, то он устранит не три, а только две степени свободы.
Появление угловых интервальных размеров
В этом году команда C3D Solver продолжила работать над темой интервальных размеров. В то же время они реализовали аналогичную функциональность для угловых размеров, которые принимают различные величины угла в определенном диапазоне.
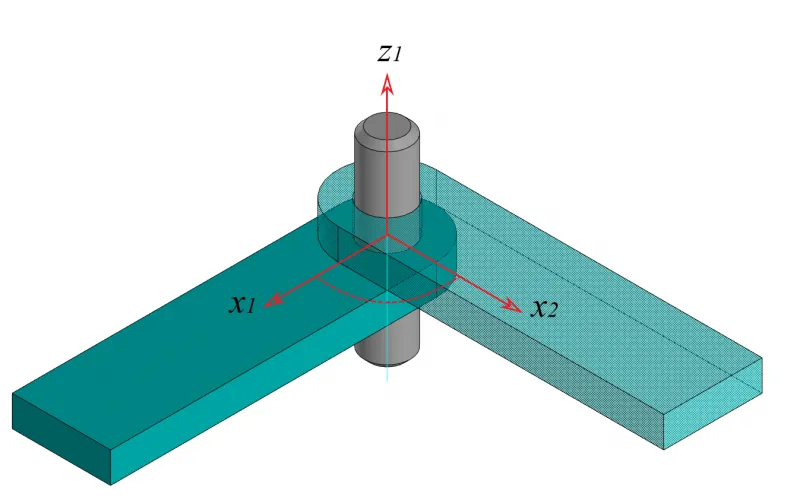
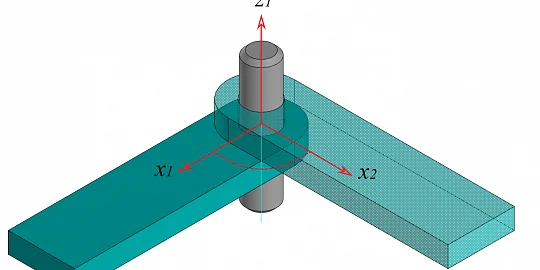
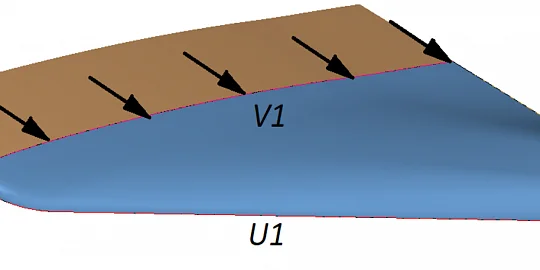
Для того чтобы новый функционал правильно отмерял размерные углы, разработчикам потребовалось переработать некоторые внутренние уравнения, задающие вращения векторов. В частности, угловой размер — это тернарное ограничение, которое принимает три объекта: два объекта, между которыми откладывается угол, и третий объект — ось вращения угла между ними (планарный подтип).
Пользователь может не указывать третий объект — ось (трехмерный подтип), тем не менее угловой размер все равно будет функционировать, как если бы эта ось вращения была задана (решатель создает такую ось автоматически). Это, в свою очередь, позволяет все виды углов привести к одинаковой области определения от 0 до 360 градусов, т.к. в трехмерном пространстве без указания оси вращения угол измеряется по кратчайшему повороту, который не превышает 180 градусов. Например, углы с величиной 270 или 90 градусов в трехмерном пространстве эквивалентны, если ось вращения не задана.
Что дальше?
В следующем году команда C3D Solver планирует реализовать еще один тип измерений (наряду с управляющим и интервальным) — вариационный размер, значением которого является [скалярная] переменная системы ограничений. Предполагается, что новое измерение удовлетворит такие потребности САПР:
1) Информационные размеры с переменной, измеряющие текущее состояние геометрии. Переменные таких измерений могут участвовать в инженерных уравнениях или в параметрической модели САПР.
2) Связывание переменных вариационных размеров друг с другом соотношениями — как правило, это линейные уравнения и пр., например, размер D2 равен половине размера D1.

Автор:
Александр Максименко
Руководитель разработки C3D Solver, C3D Labs

Автор:
Артем Максименко
Продакт-менеджер, C3D Labs