There is demand today for CAD systems advanced enough to model complex curves and surfaces, such as car bodies and high-end consumer products. Even though a CAD system could model Class A curves and surfaces, this does not mean it can provide the quality of faired G2 curves, the so-called Class F curves.
The developers at C3D Labs faced the challenge in implementing the modeling of top quality curves and surfaces. Our geometric modeling system now has a new component in the C3D Modeler kernel, the C3D FairCurveModeler, which is designed to model Class F curves.
This is the first in a series of articles about this new curve capability from C3D Labs. In part 1, we describe the key benefits of these curves and their application to engineering geometry. Part 2 discusses the F-curve support provided by our C3D Modeler, and part 3 lists case studies of products designed with C3D FairCurveModeler.
What Are Functional Curves?
Functional curves are a new type of 2D and 3D curve that enable specific performance specifications during product design. Applications of these curves are quite common and are useful for challenging projects faced in various engineering fields, such as these ones:
- Modeling airfoil wing curves with maximum lift force and minimum aerodynamic drag (see figure 1)
- Finding the smoothest road geometry for comfortable and safe vehicle travel while observing regulatory restrictions
A subclass of functional curves is known as engineering analytical curves. They offer the only optimal shape that guarantees a specific design property for the product. One such curve is the involute of circles used to design profiles of gear teeth. Another is the brachistochrone curve, which describes a curve of fastest descent for objects under the influence of gravity.
Other functional curves can be arbitrary. Such curves are locally convex (their curvature sign is fixed) or have inflection points (they have segments with different curvature signs). Additionally, functional curves can be spatial, i.e. have torsion (twist).
Let’s now consider functional curves in detail to learn how they differ from more common smooth curves.
Quality Requirements for Functional Curves
Engineering curves need to be extremely smooth. To reach this goal, these curves have a common set of requirements, regardless of the product being designed. Here are the requirements, along with our comments.
а. High order of smoothness of the curve
Smoothness is a property of a function of geometric shapes (curves, surfaces, etc.) that indicates whether the function is differentiable over the entire function domain, or whether each point of the shape has vicinity that can be defined by differentiable functions.
Splines with different orders of smoothness are used in different types of design, such as these:
- Roads are modeled with clothoid splines, as their smoothness should be of at least second order
- Camshaft lobe profiles of high-RPM engines should have a smoothness order of at least 3, achieved by plotting a continuous third-derivative curve as the first design step
- 3D curve modeling should have a third order of smoothness to ensure a continuous torsion function the curve
By analyzing the 3D curved path in moving a mass point, we see that a curve with smooth torsion has the 4th order of smoothness.
b. Minimal or no extrema of the curve
The fairness of the curve also depends on the form of the curvature graph. Let’s return to the mass point example. Under the equation of basic dynamics, the oscillation of the curvature function results in a pulsation of the centrifugal forces applied to the mass point. As a result, the trajectory shall have the minimum number of curvature extrema or the minimum number of peaks.
An excessive number of curvature extrema in engineering parts or stylish consumer products can lead to negative results in the field, such as these:
| Examples of Poor Curvature | Result |
| Excessive cam follower runout | Premature wear of the gears |
| Concentrated soil sticking in areas on the curvature of a plow (see figure 2) | Higher plow resistance and as a consequent higher energy consumption during soil cultivation |
| Extra curvature extrema on an airfoil | Undesirable airflow pulsation with higher aerodynamic drag and possible stalling |
| More frequent acceleration and deceleration during vehicle movement along a road | Higher energy consumption |
Other negative effects result in the “curved mirror effect” of outside surfaces of car and architectural forms, and improper visual perception of CGI/CAD images.
c. Low curvature variations of the curve
The curvature variation should be in some applications minimized, which means that the maximum curvature concentration needs to be limited. For example, the minimum curvature radius (maximum curvature) in road layout design is limited by the allowable vehicle speed.
The curvature variation rate is a significant quality metric. In road design, this metric indicates the rate of rise of the centrifugal force applied to a turning vehicle and is easily controlled by using clothoid segments with linear curvature function.
d. Low potential energy of the curve
It is assumed that a curve’s smoothness varies directly with its potential energy. Functional curves with low potential energy are based on the assumption that when an object with a functional surface moves at a high speed, the airflow acts as an elastic body. It takes less work to deform an elastic medium along flow paths with lower potential energy. In cases where a mass point moves along a concave curve path with friction, the work required to move it is lower for the lower potential energy of the point path.
The curve with the minimum potential energy is called the elastica (in which material regains its normal shape after distortion):
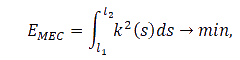
where
EMEC is the curve potential energy
k(s) is its curvature
l2 and l1 are the initial and final values of the range
Elastica can be represented as the centerline of a deformed elastic bar between two ducks (spline weights). The high quality of the elastica curve has been proved by many centuries of shipbuilding, in which flexible strips of wood (physical splines) were used to draw frames, buttock lines, and waterlines to design and build boats, and then cars and aircraft.
e. Aesthetic appeal of the curve
Apart from the objective smoothness criteria listed above, the curve quality should also be assessed from an industrial aesthetic point of view. One such an approach is to look at curve shapes that come from the mathematical features of real-life shapes, such as the outlines of butterfly wings.
To model aesthetically appealing shapes, we propose using so-called log-aesthetic curves that have linear-logarithmic curvature graphs. Many well-known spirals (such as the clothoid) are a special case of these curves. A paper1 by Ziatdinov proposes the most generalized class of curves with a monotonic curvature function, superspirals. Equations of these curves are expressed through Gaussian hypergeometric functions and numerically integrated by adaptive integration methods, such as the Gauss-Kronrod method.
However, the set of aesthetic curves includes not just log-aesthetic curves. Curves may have arbitrary complicated 2D and 3D shapes, while still being quite aesthetically appealing.
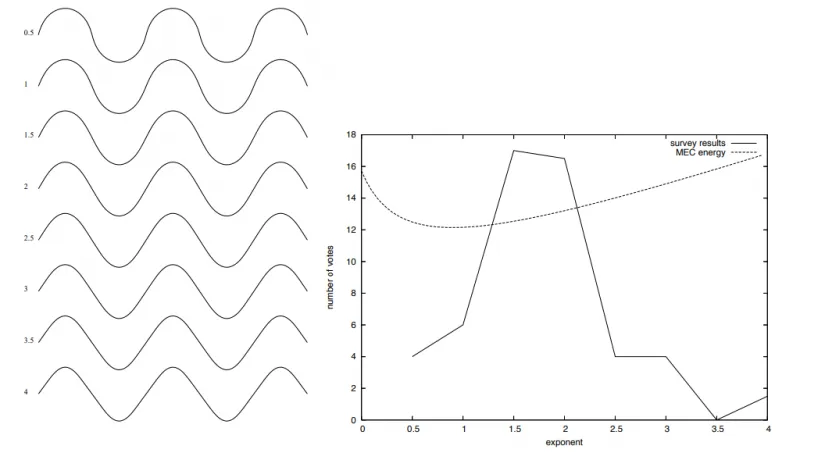
The paper’s authors believe that smoothness criteria should be a priority. An expert assessment in terms of industrial aesthetics (conciseness, integrity, expressiveness, proportional consistency, compositional balance, structural organization, figurality, rationality, dynamism, immensity, plasticity, harmony) should be used only after a fairness assessment.
In this regard, a significant work2 by Levin presents an expert assessment of the aesthetic appeal of curves with various smoothness values. The highest score is given to the curves that meet the basic requirements for functional curves, ones that simultaneously have low curvature and a low curvature variation rate (see figure 3).
Summary
Considering the above requirements for generating very smooth motion paths, we need to follow these criteria:
- A minimum number of spline path reference points and a high order of smoothness (4 or higher)
- Smooth torsion of 3D curves
- Limited maximum curvature variation values and rates of variation
- Minimization of the curves’ potential energy
Functional curves that meet these requirements are called Class F curves.
It is important to note that strict smoothness requirements mark the difference between Class F and Class A curves. The latter are used to generate highly aesthetic outside surfaces of vehicles (see figure 4). A “good” curve for generating Class A surfaces will have a curvature graph with a low number of monotonic curvature segments. This requirement can be compared to the requirement of minimizing the number of curvature extrema in functional curves.
Summing up, class A curves are used to generate surfaces in industrial design applications, while Class F functional curves are used for engineering applications. These high-quality curves are also called faired or fairing curves. These should not be mixed up with smooth curves, which are ones with the lowest quality, 1st order of smoothness curves.
1 Ziatdinov, R. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function // Computer Aided Geometric Design. 2012. Vol. 29. No. 7. Pp. 510–518.
2 Levien, R. L. From Spiral to Spline: Optimal Techniques in Interactive Curve Design. PhD thesis, University of California, Berkeley, 2009.